library(tidyverse)
library(knitr)2 Extract Model from geom_smooth model
Example code to extract x and y values from a geom_smooth.
The practical example used her is to take discrete values of a value n at monthly intervals across a year. The geom smooth is used to draw a smoothed line across the chart. Then the values of n are extracted from the model before being floored so that we can estimate a new value for each month.
This would be helpful where you have a situation in which there’s a month missing in the middle, or where there’s an outlier or two. You could achieve the same thing using a regression, but this is a useful approach that ultimately leans back on to polynomial regressions.
Make a dummy data set with 11 observations and increasing number
df<-tibble(
month=1:11,
n = c(100,140,200,260,360,470,560,630,770,990,1100)
)
kable(df)| month | n |
|---|---|
| 1 | 100 |
| 2 | 140 |
| 3 | 200 |
| 4 | 260 |
| 5 | 360 |
| 6 | 470 |
| 7 | 560 |
| 8 | 630 |
| 9 | 770 |
| 10 | 990 |
| 11 | 1100 |
Make a ggplot object with a geom_smooth()
p <- ggplot(df, aes(month, n))+geom_smooth(method = "lm") +geom_point()
p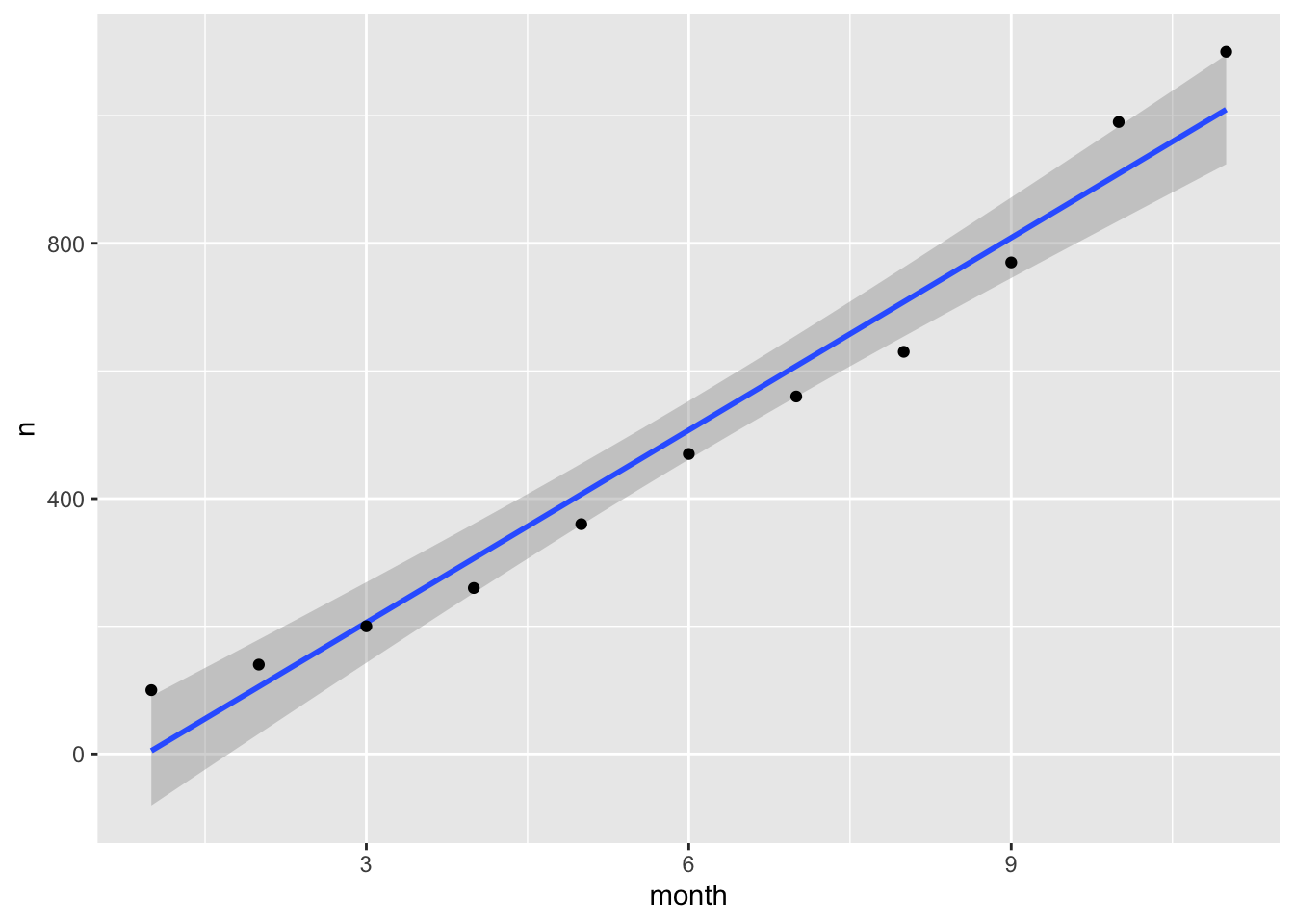
Use ggplot_build to find the code behind the curve - the first element of data in the result is the geom_smooth curve
pp<- ggplot_build(p)$data[[1]] %>%
rename (
month = x,
n = y
)
kable(pp)| month | n | ymin | ymax | se | flipped_aes | PANEL | group | colour | fill | linewidth | linetype | weight | alpha |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.000000 | 5.00000 | -80.699424 | 90.69942 | 37.88394 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 1.126582 | 17.71577 | -66.439648 | 101.87118 | 37.20140 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 1.253165 | 30.43153 | -52.191714 | 113.05477 | 36.52410 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 1.379747 | 43.14730 | -37.956292 | 124.25088 | 35.85232 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 1.506329 | 55.86306 | -23.734100 | 135.46022 | 35.18640 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 1.632911 | 68.57883 | -9.525902 | 146.68355 | 34.52666 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 1.759494 | 81.29459 | 4.667484 | 157.92170 | 33.87347 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 1.886076 | 94.01036 | 18.845183 | 169.17553 | 33.22721 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 2.012658 | 106.72612 | 33.006263 | 180.44598 | 32.58830 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 2.139241 | 119.44189 | 47.149728 | 191.73405 | 31.95718 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 2.265823 | 132.15765 | 61.274512 | 203.04079 | 31.33431 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 2.392405 | 144.87342 | 75.379479 | 214.36736 | 30.72021 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 2.518987 | 157.58918 | 89.463417 | 225.71495 | 30.11540 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 2.645570 | 170.30495 | 103.525033 | 237.08486 | 29.52046 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 2.772152 | 183.02071 | 117.562952 | 248.47848 | 28.93599 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 2.898734 | 195.73648 | 131.575706 | 259.89725 | 28.36265 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 3.025317 | 208.45224 | 145.561741 | 271.34275 | 27.80112 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 3.151899 | 221.16801 | 159.519403 | 282.81662 | 27.25213 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 3.278481 | 233.88377 | 173.446945 | 294.32060 | 26.71646 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 3.405063 | 246.59954 | 187.342517 | 305.85656 | 26.19492 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 3.531646 | 259.31530 | 201.204173 | 317.42644 | 25.68837 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 3.658228 | 272.03107 | 215.029868 | 329.03227 | 25.19772 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 3.784810 | 284.74684 | 228.817460 | 340.67621 | 24.72391 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 3.911392 | 297.46260 | 242.564717 | 352.36048 | 24.26794 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 4.037975 | 310.17837 | 256.269325 | 364.08741 | 23.83081 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 4.164557 | 322.89413 | 269.928894 | 375.85937 | 23.41360 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 4.291139 | 335.60990 | 283.540975 | 387.67882 | 23.01738 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 4.417721 | 348.32566 | 297.103075 | 399.54825 | 22.64325 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 4.544304 | 361.04143 | 310.612678 | 411.47018 | 22.29233 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 4.670886 | 373.75719 | 324.067267 | 423.44712 | 21.96573 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 4.797468 | 386.47296 | 337.464355 | 435.48156 | 21.66454 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 4.924051 | 399.18872 | 350.801513 | 447.57593 | 21.38985 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 5.050633 | 411.90449 | 364.076404 | 459.73257 | 21.14269 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 5.177215 | 424.62025 | 377.286822 | 471.95368 | 20.92402 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 5.303797 | 437.33602 | 390.430726 | 484.24131 | 20.73476 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 5.430380 | 450.05178 | 403.506283 | 496.59728 | 20.57571 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 5.556962 | 462.76755 | 416.511896 | 509.02320 | 20.44759 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 5.683544 | 475.48331 | 429.446245 | 521.52038 | 20.35096 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 5.810127 | 488.19908 | 442.308311 | 534.08985 | 20.28629 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 5.936709 | 500.91484 | 455.097402 | 546.73229 | 20.25387 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 6.063291 | 513.63061 | 467.813167 | 559.44805 | 20.25387 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 6.189873 | 526.34638 | 480.455607 | 572.23714 | 20.28629 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 6.316456 | 539.06214 | 493.025071 | 585.09921 | 20.35096 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 6.443038 | 551.77791 | 505.522253 | 598.03356 | 20.44759 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 6.569620 | 564.49367 | 517.948170 | 611.03917 | 20.57571 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 6.696203 | 577.20944 | 530.304144 | 624.11473 | 20.73476 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 6.822785 | 589.92520 | 542.591770 | 637.25863 | 20.92402 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 6.949367 | 602.64097 | 554.812883 | 650.46905 | 21.14269 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 7.075949 | 615.35673 | 566.969522 | 663.74394 | 21.38985 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 7.202532 | 628.07250 | 579.063895 | 677.08110 | 21.66454 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 7.329114 | 640.78826 | 591.098338 | 690.47819 | 21.96573 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 7.455696 | 653.50403 | 603.075278 | 703.93278 | 22.29233 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 7.582279 | 666.21979 | 614.997206 | 717.44238 | 22.64325 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 7.708861 | 678.93556 | 626.866636 | 731.00448 | 23.01738 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 7.835443 | 691.65132 | 638.686086 | 744.61656 | 23.41360 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 7.962025 | 704.36709 | 650.458047 | 758.27613 | 23.83081 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 8.088608 | 717.08285 | 662.184970 | 771.98074 | 24.26794 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 8.215190 | 729.79862 | 673.869244 | 785.72799 | 24.72391 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 8.341772 | 742.51438 | 685.513182 | 799.51559 | 25.19772 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 8.468354 | 755.23015 | 697.119018 | 813.34128 | 25.68837 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 8.594937 | 767.94591 | 708.688892 | 827.20294 | 26.19492 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 8.721519 | 780.66168 | 720.224851 | 841.09851 | 26.71646 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 8.848101 | 793.37745 | 731.728840 | 855.02605 | 27.25213 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 8.974683 | 806.09321 | 743.202708 | 868.98371 | 27.80112 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 9.101266 | 818.80898 | 754.648204 | 882.96975 | 28.36265 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 9.227848 | 831.52474 | 766.066979 | 896.98250 | 28.93599 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 9.354430 | 844.24051 | 777.460591 | 911.02042 | 29.52046 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 9.481013 | 856.95627 | 788.830505 | 925.08204 | 30.11540 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 9.607595 | 869.67204 | 800.178098 | 939.16598 | 30.72021 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 9.734177 | 882.38780 | 811.504661 | 953.27094 | 31.33431 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 9.860760 | 895.10357 | 822.811408 | 967.39573 | 31.95718 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 9.987342 | 907.81933 | 834.099474 | 981.53919 | 32.58830 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 10.113924 | 920.53510 | 845.369924 | 995.70027 | 33.22721 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 10.240506 | 933.25086 | 856.623755 | 1009.87797 | 33.87347 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 10.367089 | 945.96663 | 867.861900 | 1024.07136 | 34.52666 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 10.493671 | 958.68239 | 879.085233 | 1038.27955 | 35.18640 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 10.620253 | 971.39816 | 890.294571 | 1052.50175 | 35.85232 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 10.746835 | 984.11392 | 901.490680 | 1066.73717 | 36.52410 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 10.873418 | 996.82969 | 912.674276 | 1080.98510 | 37.20140 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
| 11.000000 | 1009.54545 | 923.846030 | 1095.24488 | 37.88394 | FALSE | 1 | -1 | #3366FF | grey60 | 1 | 1 | 1 | 0.4 |
Plot the data from what we just extracted, to prove the principle.
ggplot() +
geom_smooth(aes(month, n), df,color="blue",lwd=2)+
geom_line(aes(month, n), pp,color="red",lwd=1)
To find a start of month amount, find the floor of each integer on x axis
pp$month<-floor(pp$month)Remove replicates and select the values of x and y
pp <- pp %>% mutate(dup = duplicated(month)) %>%
filter(dup==FALSE) %>%
select(month,n)
df<-bind_cols(df,pp[,2])
kable(df)| month | n | …3 |
|---|---|---|
| 1 | 100 | 5.0000 |
| 2 | 140 | 106.7261 |
| 3 | 200 | 208.4522 |
| 4 | 260 | 310.1784 |
| 5 | 360 | 411.9045 |
| 6 | 470 | 513.6306 |
| 7 | 560 | 615.3567 |
| 8 | 630 | 717.0829 |
| 9 | 770 | 818.8090 |
| 10 | 990 | 920.5351 |
| 11 | 1100 | 1009.5455 |